一般的に数学というものには明確な答えが用意されています。しかし、数学界には数学者を二分する「眠り姫問題」という思考実験があります。この「眠り姫問題」は2000年に話題になって以来、未だに納得のいく回答が見つかっていません。そんな問題の詳細について、海外メディア「scientificamerican」が解説しています。
関連:認知症を何十年も遅らせた〝特異な遺伝子〟が発見される
*Category:
「眠り姫問題」が複雑な理由とは?

「眠り姫問題」のルールは下記の通りです。
実験の参加者である眠り姫は、実験の内容を全て説明され、一日経過後、薬を投与され日曜日に眠りにつきます。そして、眠り姫が眠っている間に一度だけ公正なコインが投げられます。
- コインが表であった場合、眠り姫は月曜日に目覚めさせられ、「コインが表だった確率は幾らか?」という質問をされたのち、再び薬を投与され眠りにつきます。
- コインが裏であった場合、眠り姫は月曜日に目覚めさせられ、「コインが表だった確率は幾らか?」という質問をされたのち、再び薬を投与され眠りにつきます。そして翌日の火曜日にも目覚めさせられ、質問されたのち、再び薬を投与され眠りにつきます。
どちらの場合でも水曜日に起こされ実験は終了します。ここで重要なのは、睡眠薬のせいで、眠り姫には前に起こされたかどうかの記憶がないことです。そのため、目覚めたときに、今日が月曜日なのか火曜日なのか区別がつかないのです。
眠り姫の立場では、目を覚ますと、今日が何日なのかも、以前に起こされたことがあるのかどうかもわかりません。つまり、実験の理論的な経過しか知らないということです。
アメリカの哲学者デイビッド・ルイスは、コインの裏表の確率は1/2であると考えました。
眠り姫は、事前に実験の詳細を説明されて以降、実験中に新しい情報を受け取ることはできません。実験前の彼女にとって、表であった確率はP(表)= 1/2であり、実験中に目覚めたときに新たな情報を得ることもできないため、P(表)= 1/2という確率も変わらないはずです。
一方、プリンストン大学の科学哲学者アダム・エルガは、裏表の確率は1/3であると考えました。
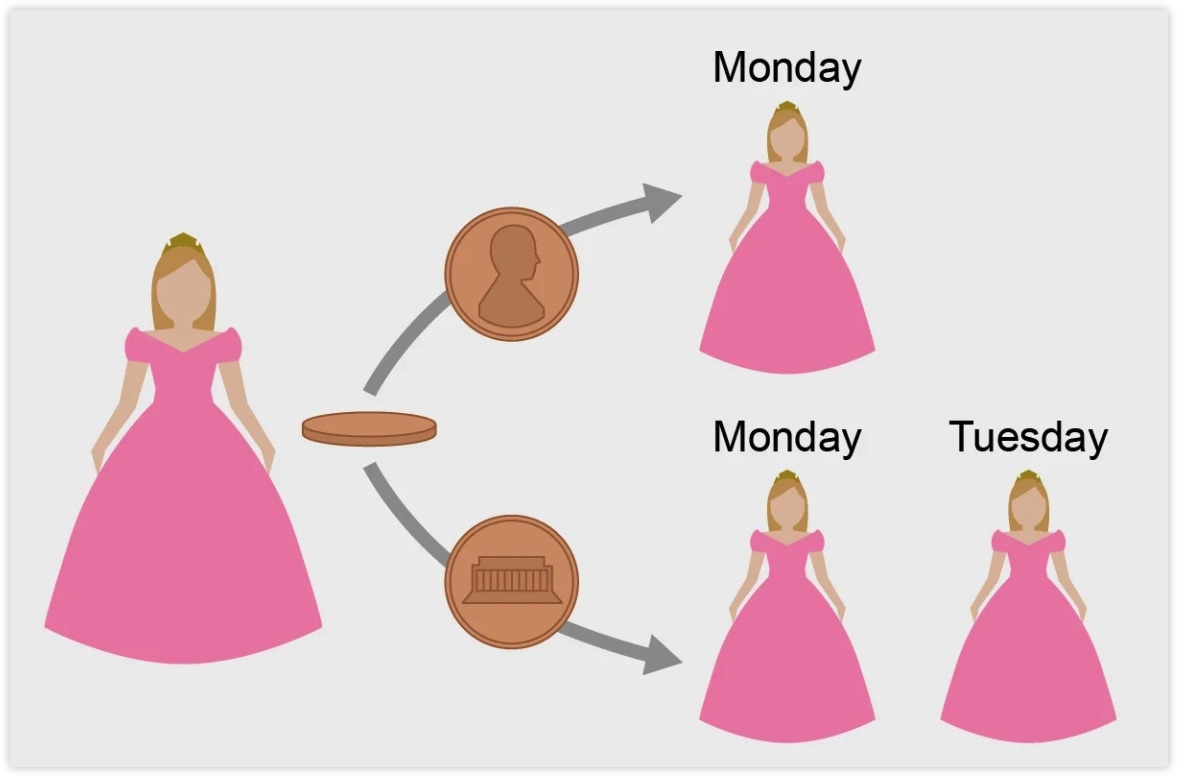
眠り姫が目覚める可能性は3パターンあり、その内コインが表になるのは1度だけです。
- コインが表で、目覚めるのが月曜日
- コインが裏で、目覚めるのが月曜日
- コインが裏で、目覚めるのが火曜日
これらの3つの状況のうち、コインが表である状況は1つしかありませんが、コインが裏である状況は2つあります。つまり、眠り姫が目覚めたときに「コインが表だった確率は幾らか?」と質問された場合、その答えは1/3になるということです。
ただし「1/2」という考え方と「1/3」という考え方、どちらが正解なのかは明確に分かっておらず、今もなお議論が行われているとのことです。この問題は、哲学者や数学者が意思決定や確率について考える際の良い思考実験とされています。